| CHAPTER FOUR | |
| NON DETERMINISM AS A PARADIGM FOR UNDERSTANDING THE USER INTERFACE | |
Alan Dix |
|
Although this chapter primarily presents conceptual and pragmatic ideas about non determinism in user-interfaces, there is another, higher level, and more important point to it. This chapter exemplifies the subtle interweaving of formal and informal reasoning, the way formal analysis can lead to new insights which influence the informal.
We start with an examination of problems arising from several formal models of ineractive systems.Chapter 5 [Harrison and Dix 1990] gives a fairly detailed account of one such model, however, here our treatment will be less formal, only considering those features essential for the present discussion. These features lead us to consider non deterministic models in order to express properties of interest. These models are non deterministic in a purely formal sense; the rest of this chapter considers the repercussions non determinism has on our understanding of the user intterface.
Non determinism contradicts the general feeling that computer systems are deterministic, following a fixed set of instructions, so we might wonder whether there is any real meaning to this use of the term non-determinism, or whether it is a useful, but essentially meaningless, formal trick.
Here, we shall demonstrate four things about non-determinism in user interfaces:
Sections 4.4 and 4.5 deal with the first of these points. The first of these shows that non-determinism is in fact a common experience of users, and we focus on the notion of behavioural non-determinism in order to square this with the normal deterministic model of computation. The next section then catalogues various sources of non-determinism in the user interface.
Further sections show how users, abetted by the designers of systems, can deal with non determinism. The final point of section 4.6 reminds us how non determinism can be useful in the specification of systems, however this non determinism is not intended to be a facet of the actual system, only a tool for development. Section 4.7 goes beyond this giving an example of how non determinism might be deliberately introduced into the user interface to improve performance. Without being prepared - by noting how supposedly deterministic systems behave as if they were non-deterministic - the deliberate introduction of non determinism would seem preposterous! Instead we are able to assess it impartially and see how it may actually reduce apparent non-determinism for the user.
This last section is of a semi-formal nature, but the preceeding discussion will be essentially informal. So that the overall structure of the chapter is:
To some extent the overall structure of the chapter (formal models; informal analysis; semi-formal application) is the opposite of the normal presentation where an informal problem leads to a formal statement and analysis, but it reflects the true historical development of the work. The formal models of course did arise originally from informal consideration of the systems they describe, but the issue of non-determinsim, and the recognition of it in various guises arose directly from the formal analysis. Having done that however, it didn't remain in the formal sphere, but enabled understanding beyond the aspects formally modelled.
Several different interaction models have been developed at York to understand and express properties of various styles of interaction. These are abstract formal models: abstract in iorder to be generic over a range of similar systems and formal in order to be amenable toi analysis. Here we are going to consider briefly three of these interaction models:
In any particular system, we may want to apply properties expressed over several of these models and we could simply map them all onto the system independently, however it is clearly sensible to consider how these inter-relate at the abstract level, and if possible relate them all back to the general PIE model. This process will require a non deterministic version of the PIE model.
More details about these models and the principles that can be defined, using them can be found in the papers cited above, and in my thesis [Dix 1987b].
The PIE model is a very simple model of single stream input/output interactive
systems, The user enters a stream of commands from a set ![]() D
D![]() R
R![]() E
E
This model is used to express simple properties applicable to nearly all interactive systems. Although it is a simple model, it is surprising how complex the analysis can be! One of the first principles considered was related to predictablity. I have been using the system, I go away for a cup of tea, and upon returning have forgotten where exectly I am in the dialogue. Is there sufficient data available for me to proceed. This has been addressed at various levels of complexity and abstraction, but one of the simplest requirements is that the system be predictable
This says that if two systems have the same current effect, then whatever further commands are entered, they will stay the same. Ifp,q,r
P I( p ) = I( q )
I( pr ) = I( qr )
The above model, does not tell us how long we have to wait for an effect, only what that effect will be when it comes, that is it is a steady state model. It does not allow us to describe real time phenomena, such as the buffereing (or lack of buffering) of user input, or display strategies such as intermittant update (when some intermediate displays are skipped when typing fast) or partial update (when part of the screen is kept up to date, but the rest is allowed to lag behind the typing).
We can augment the model to allow us to describe real time phenomena by including
in the possible inputs at any time the possibility of no input (represented
by ![]() { τ }
{ τ }![]() E
E
The user will be unaware of detailed timings (with a clock operating at MHz!),
and it is only some abstraction of this temporal behaviour which is apparent.
Clearly from any sequence from
Isteady( h ) = Iτ ( h τ τ τ .. )
Having removed timing from the temporal system the result is likely to be
non-deterministic. For instance take the bufferless typewriter which requires
a single time interval after each character in order to reset itself and ignores
any characters being entered too fast. In this case The interpretation function is defined as follows,
Clearly we need a non-deterministic version of the PIE model to model such
behaviour.
A similar problem arises when considering the representation of windows. We
can create a model similar to the PIE model to represent windowed systems. We
associate with each window a label or handle (from a set The whole system may be regarded as a PIE with a command set of
If we "freeze" all other windows we can give the functionality of a window
This definition is not very useful:
it's not very interesting knowing the functionality of a window system when you
only use one window!
What we really want to know is the functionality of each window when other
windows are being used also.
To do this we would consider the possible effect of commands
We will now consider non deterministic generalisations of the PIE model. There
are various ways of modelling non-determinism, but one of the simplest is to
substitute for some value a set of possible values. However, we have to be careful
to choose the right representation of our model, and the right values to substitute.
The simplest option is to assign to each input set of possible effects. That
is we modify the signature if the interpretation to
Does this describe a system that starts off with a value of 0 or 1 and retains
this value no matter what the user enters,
does it represent a system that makes an independent choice after each command,
or is it something in between.
On the basis of the information given, we cannot decide.
We therefore need to consider the trace of all effects generated by a command.
For any deterministic PIE we can always define a
new interpretation That is we define an interpretation giving the entire history of effects for
each command history. This is the appropriate function to generalise for non-determinism
yielding an interpretation
We can see that necessary conditions for a valid interpretation From now on we will call a triple <
We can say that a ND-PIE is deterministic if for all
If we don't want our ND-PIEs to have input languages, then we have to put more
restrictions on
We can now use the ND-PIE to represent the non-deterministic functionality
we required in section 4.2.1.
That is:
With this definition the example of the typewriter which misses characters
typed too quickly gives us:
Not only can we now define this functionality, but it gives us a new way to
look at the system.
A perfectly buffered system with total update (ie. no intermediate displays
skipped)
is precisely a system where
We consider using a window (with handle
We have seen that properties over temporal models and handle spaces can be
given statements as determinacy properties of ND-PIEs.
Are there any interesting ND-PIEs that can be abstracted from simple PIEs?
We considered the simple predictability property that a PIE is monotone
if:
One other ND-PIE suggested by the definition of
A specific case of this is where the interpretations are PIEs representing the
"same" system with different start data.
If we consider the red-PIE, we will often have the case where there is a
"bundle" (tray!) of PIEs, each indexed by an element of the result,
The ND-PIE generated from these interpretations:
We have seen how a non-deterministic model has been useful in unifying the
description of various properties in diverse models.
The examples above share one common feature: in each case, the deterministic
model is viewed via an abstraction which corresponds to losing some part of
the available information. This leads to non deterministic behaviour. In each
case the non deterministic model used to capture this behaviour was the ND-PIE,
however this is largely because the various models were derivatives and extensions
of the basic PIE model. Different flavours of model could be dealt with similarly
using different non-deterministic models and perhaps using different methods
of expressing the non-determinism.
When viewed in the light of the previous discussion, properties such as predictability
and non-interference of windows become efforts to control non determinism, Either
they assert that in certian circumstances the effect is deterministic, or give
procedures to resolve it.
In the last section, we found that formal models of non-determinism are useful
to describe certain abstract properties of interactive systems, however we were
left wondering whether this formal construction held any meaning for the user.
We accept that the internal workings of some systems will be non-deterministic,
especially where concurrent processes are used,
and even that some specialist applications like simulations and certain
numerical methods will involve random number generation,
but surely most real systems have a deterministic external interface.
Do users perceive computers as deterministic?
In fact the opposite is the case, most users expect a degree of randomness from
the systems they use.
Time and again they will shrug their shoulders in bewilderment,
"Oh well it didn't work this time, I'll try the same thing again, it may work
now."
The apparently random behaviour of such systems conflicts with the alternative
model of the computer as a deterministic machine relentlessly persuing its
logical course.
Some users are able to cope with this.
Expert users may treat this as a challenge, puzzling over the behaviour and
experimenting until a logical reason is found,
pragmatists will accept the occasional strangeness circumventing it,
and more awestruck users will regard it as part of the magic and mystery of
modern technology.
Others may have a more negative reaction.
The self-confident may react "this is silly" and loose all confidence in the
computer,
the self-depreciating may respond "I'm silly" attributing their problems to
their own lack of understanding, and possibly retiring from further use.
Phrased in these graphic terms the problem seems extreme and demands
investigation, but how can it be that thoroughly deterministic programs give
rise to this apparent randomness.
Very few systems are really random, even random number generators are usually
based on deterministic algorithms, ERNIE being a possible exception.
Programs that rely on external events could be classified as non-deterministic,
for instance the time when a printer signals that it has emptied its buffer,
but even then the printer itself will probably behave deterministically.
In fact what is usually termed non-determinsim reflects the things that the
programmer either doesn't know or doesn't want to know.
In other words, it is programmer centred.
We could classify non-determinsim into several levels, depending on what they
appear non-deterministic to.
The theme that comes out of the above is that non-determinism is relative,
relative to knowledge and to reasoning abilities.
What should a user centred view of non-determinism be? If we imagine two
systems, they each have two possible prompts, each day they choose a different
prompt for the day. One system bases its choice on whether the number of days
since 1900 is prime or not, the other on the decay of a slightly radioactive
substance. From the programmers point of view (and the computers), we would
say that the former is deterministic and the latter not. From the user's point
of view the two systems display equally non-deterministic behaviour.
That is, as the user sits at the bottom of the hierarchy of knowledge, all
the forms of non determinsim are equally random, and should be treated equivalently.
That is we are going to take a behavioural view of non-determinism. This
recognises that some system may be "really" deterministic and others may be
"really" non-deterministic according to some definition, but if they behave
the same, we will regard them as equally non-deterministic. Not only does this
mean that we regard some "really" deterministic systems as deterministic, but
also the other way round. For instance, if we had a music system with some random
"noise" that lead to errors of 1 part per million in the frequency of notes,
we would regard the system as being deterministic as the difference in behaviour
would be undetectable.
One could demand tighter views of non-determinism, but for the purposes
of this chapter we will adopt the behavioural one. Again, one could use a
weaker word to represent behavioural non-determinism however the use of such
a charged word concentrates the mind wonderfully.
In the last section we decided that, taking a behavioural view of non-determinism,
it did make sense to describe interface behaviour in these terms. In doing
so, we introduced some examples to argue the point. In this section we will
catalogue informally some of the sources of non-determinism in the user interface,
giving more examples on the way. We will study these sources of non-determinism
in six sub-sections under several headings:
The first two of these cover the informal equivalents of the two formal problems
that started this chapter in sections 4.2.2 and 4.2.3. The second two consider
problems that appear even in the steady state functionality of single windowed
systems, and cover lack of knowledge about what you are dealing with
and how you should do it. These correspond to some of the ND-PIEs
we considered in section 4.3.3. The last two are to do with the more complex
ways that human limitations can give rise to apparent non determinism. These
two could be thought of as "the user's fault", but the system designer cannot
wriggle out of it so easily, good system design should take into account the
inevitable human limitations of its users.
I'm sure this list is not complete however it gives a broad spectrum of
different types of non-determinism to which the reader can add.
A variety of problems that users experience can be viewed as manifestations
of non determinism. When a user types quickly, intermittent and partial update
strategies produce different output than if s/he had typed more slowly. If the
user is unaware of this exact timing, then the system's behaviour is apparently
non-deterministic. This non-determinism is usually deemed acceptable since the
final display does not depend on the exact timing, and further, spells of fast
typing may be regarded as single actions anyway. Intermittent update could be
said to be less non-deterministic than partial update since at least all its
intermediate displays would have arisen with slow typing. On the other hand
a portion of the screen in partial update is always exactly as it would be if
the machine were "infinitely fast", and this portion is therefore totally deterministic.
Similarly the problems associated with slow machines and buffering can be
thought of as non-determinism. A machine that doesn't buffer and loses characters
typed too quickly could be regarded as non-deterministic on this score. This
is exactly the non determinism captured by the formal model at the beginning
of this chapter. However a system with buffering can lead to a non-deterministic
feedback loop between user and computer, leading for instance to cursor tracking
(where the user continually overshoots with the cursor)..
Scheduling of multiple processes leads to non determinism. If for some reason
a system makes explicit or implicit use of real time, then, when running on
a time share computer, the run times of its components and hence possibly its
functionality, will be non-deterministic. More often than not this dependency
on real time will be in the assumptions made about the relative speeds of certain
components, or in the assumption that two statements following one another will
be executed immediately, one after the other. The most innocuous case of this
is when several concurrent processes print messages to the terminal in random
order.
Again the problem of sharing can be regarded as one of non-determinism,
reflecting exactly the formal treatment. For instance as I transact with one
process which is my focus of interest, other processes may print error messages
on the screen. Because I am preoccupied with the focal process, I may have
forgotten that the others were running and thus be temporarily confused. In
this case I would not remain confused for long, as I would remember what other
processes were running (or ask the system), and infer their behaviour. Thus
the non-determinism could be resolved, but not soon enough to stop me acting
(potentially disastrously) on a changing system.
This situation is in the middle of three levels of sharing. Each of these
types of sharing can lead to non-determinism.
Single actor - multiple persona. The user is simultaneously involved
(perhaps via windows) with several dialogues, which may share data. When switching
from one dialogue to another, he may forget that actions in one dialogue may
have repercussions in the other, thus causing apparent randomness. Literally
the right hand may not know what the left is doing.
Single controller - several actors. The user sets off several concurrent
processes that affect data common to each other and to the user's current
view. This is the original case given above, and differs from the single actor
case in that changes may actually occur as the user is actively involved in
a dialogue, rather than during interruptions to the dialogue. Because of this
it is apparently more non-deterministic since the system is changing as one
tries to manipulate it.
Several independent actors. This is the case of the multi-user system
where not only are several things happening at once, but they are not under
your control. This is the most random of all, since the machine processes
are at least in principle predictable, but from your point of view the other
users are fundamentally non-deterministic processes.
A user has a program on a system which was written a long time ago, the exact
contents of it is now forgotten. He wants to make changes to this program and
invokes his favourite editor by entering the command "edit prog".
This is an example of data uncertainty; the user does not know the
exact value of the data on which he is going to operate, and a major goal of
the interactive session is to reduce the uncertainty, perhaps by scrolling through
the file to examine it. This corresponds to the ND-PIE generated
from the bundle of PIEs in section 4.3.3.
Data uncertainty is of course common. The example given is typical of uses
over many different types of task. However it is not so much a problem in
itself as it is expected: we do not expect to know all the data in a computer
system by heart. The importance is in the user's ability to discover the information,
that is in the resolution of the non-determinism, a point we shall
return to in the next section.
Consider the following two situations
In the first situation, the exact nature of the data is known and it is procedural
uncertainty from which the user suffers. She will look for clues using the
knowledge she has of editors on the system. The editor fills the entire screen
so it can't be a line editor like "ed", she surmises. Neither can it be mouse
based, like "spy", for it doesn't have menus all over the place. It could be
either of the screen editors "ded" or "vi". Tentatively she types in a few characters
to see if they're inserted in the text. The editor beeps at her a few times,
then deletes half the text ... now she knows it's definitely "vi".
This form of procedural uncertainty is captured by the ND-PIE
which chose between a set of interpretation functions. It is interesting that
the two situations which appear quite different informally, have such a similar
informal definition.
The second case is another example of procedural uncertainty of a less extreme
and more common form!
As previously stated, one of the causes of non-determinism is lack of knowledge.
This is exacerbated by the fact that people forget. Thus as the user attempts
to amass information in order to resolve the non-determinism, her efforts are
hampered by her limited memory. A designer must consciously produce features
which take account of this. These could include general features, such as an
online memo-pad and diary, or more system-specific ones. Further the user is
likely to interpolate the gaps and be unaware of which information is known
and which is inferred. This process is distinct from forgetting and we shall
call it degradation of information The designer may need be aware of
where such degradation is likely and actually force this information to the
user's attention.
We are all familiar with the idea of capture, where for example one walks
home without noticing when one intended to go to the railway station in the
opposite direction. This occurs in computer systems where commonly used sequences
of keys can take over when one intends to use another similar sequence. A
similar process can also occur at the conceptual level. For example in a display
editor where long lines are displayed over several screen lines, the cursor
up key might mean move up one screen line or one logical line. As most logical
lines will fit on the one screen line the difference may not be noticed. Later
when a long line is encountered the action of the system may appear random
to a user who has inferred the wrong principle.
Of the six headings which we've considered, the first four can be be given
formal expression, to some degree or other, using the models developed in
this and previous chapters. The last two would require a more sophisticated
model of human cognition, with its attendant problems of robustness. There
is an obvious parallel between data uncertainty and degradation of information
and between procedural uncertainty and conceptual capture. However the second
of each pair is far more dangerous. The major problem with both these situations
when compared to procedural and data uncertainty is that the user may not
be aware of the gaps in her knowledge. The situation where a user doesn't
know something and knows she doesn't know it is still non-deterministic,
but the situation where the user thinks she knows what the system is going
to do and then it does something completely different is downright random.
We could say that failure in knowledge is far less critical than failure in
meta-knowledge.
We have seen that non-determinism is a real problem in the user interface,
and that it has many causes. How can we deal with the problems of non determinism.
We will consider four options in turn:
The most obvious way of dealing with non-determinism is to make sure it
never arises. This can be done by designing a system with this in mind, or
by adding functionality afterwards. We have already seen examples of this:
In both these solutions, we add information to the interface in order to
avoid non-determinism. This is of course a general technique restricted only
by the display capacity. For instance, if procedural uncertainty is the fault
of hidden modes, then we can make the modes visible via a status line.
We can attempt to avoid conceptual capture by making sure the models we
use are either exact matches of the user's model or else where they match
and where they don't is made obvious. This is of course very difficult advice
to follow as it is difficult to predict what model the user will infer for
the system. However systems that propose a model (such as the desktop) but
fail if the user follows it too far are obvious candidates for improvement.
Another situation it would warn us to avoid is where two sub-subsystems have
apparently similar semantic behaviour, but later diverge.
In most systems of any complexity it would be unreasonable to expect complete
removal of non-determinism, however these techniques can reduce the non-determinism
or remove some aspect of it.
Assuming the user is in a situation of non-determinism he can try to resolve
that non-determinism, attempting by observation or experiment to reach a deterministic
situation.
Data uncertainty is an obvious candidate for this, and the concept of strategies
introduced in [Dix and Runciman 1985] can be thought
of as an attempt to resolve the non-determinism. When applied to result
predictability it is precisely the resolution of data uncertainty. The
use of the strategy for full predictability can be seen as the resolution
of both data uncertainty about the result and about internals such as cut/paste
buffers, but also the resolution of things such as mode ambiguity.
The designer can help the user in the resolution of data ambiguity by reducing
the conceptual and memory costs of strategies. This is aided by the fact that
the user will only want to discover some part of the information. Typical
techniques include:
Procedural uncertainty is more difficult to resolve. Help systems can be
thought of as a way of resolving procedural uncertainty, however they do of
course have to make major assumptions about how much the user knows already.
The one sort of procedural uncertainty that the help system definitely cannot
resolve, is the method for invoking help. Underlining the need to use consistent
and obvious rules for this (permanent icon, dedicated labelled key or the
use of "h" or "?".)
Rather than try to remove non-determinism completely, we can try to control
it so that the non-determinism experienced is acceptable in some way. This
can obtain at the local or the global level. That is we can ask for complete
determinism over a part of the system, or merely that some rules always apply
for the system as a whole. We consider the local level first.
It is said that you ought to be able to use a system with your eyes shut.
Extending this analogy a bit, we could observe that blind people are able to
navigate a familiar room quickly and confidently whereas they would use a totally
different strategy for navigating a busy street. Similarly, when using a computer
conferencing facility one might be able to touch type because the layout of
the keys is fixed, and attention is fixed on the screen where unexpected changes
will occur. Thus in computer systems, as in real life we need a solid base of
determinacy in order to be able to concentrate on those areas where non-determinacy
will occur. We call this requirement deterministic ground. Record and
file locking facilities are an example of how we might for a period enforce
determinacy on a shared domain. Similarly protection mechanisms offer a more
permanent way of ensuring some level of determinacy. However if we look at the
three levels of sharing mentioned in section 4.5.2, we see that only the multi-actor
case is helped by having private files. So if I have several windows, or have
some background jobs running, they are all the same user, and hence the file
system protection would fail to protect me from myself. As an example of this
breakdown of security, consider the semantics of the line printer spooler. In
some systems, the print command does not make a copy of the file to be printed
in a system spool area, but merely makes a note of the request and the file
to be printed. The user, however, after issuing the command may reach closure
on that operation and then later go on to modify or even delete the file to
be printed. Perhaps one could extend protection mechanisms to include files
private to tasks and windows?
At the global level the effects of sharing are controlled by the accepted
procedures that are used for updating them. Some of these enshrined in the
software, and some in organisational and social conventions. For instance,
today my bank's teller machine might read £300, however tomorrow it
may read only £20. If I hadn't kept a close tally on my spending, I
might not have expected the change and I would regard the change as essentially
non-deterministic; however I would have enough faith in the banking system
to believe the change due to some of my cheques clearing. If this belief were
not widely held the non-determinacy of bank balances would become unacceptable
and the banking system would collapse. Similarly early in a day a travel agent
may notice 5 seats free on a particular flight, later in the day, on trying
to book one for a customer, the request might be refused. The conclusion drawn
is that some one else has booked the seats in the meantime. Thus we rely on
the semantics of others transactions to make the apparent randomness of our
view of data acceptable. If the changes we observe in the data are not consistent
with our understood semantics we will loose confidence in the data.
I would argue therefore that in order to understand the problems of sharing
from a user oriented view, we should concentrate on defining the semantically
acceptable non-determinism of a system. That is we are prepared to accept
limited non-determinism We can apply this to other fields. For instance,
if we look at buffering strategies. A perfectly buffered system may well be
non-deterministic because the screen does not reflect the current state of
affairs, however we might regard this as acceptable. In contrast a word processor
which ignored all typeahead would be regarded as exhibiting unacceptable non-determinism.
The predicate describing perfect buffering is a limit to the non-determinism
sufficient to make it acceptable. Similarly, we may not be too worried about
the exact strategy a text editor uses when rearranging the display when the
cursor hits the screen boundaries. It would be unacceptable if the cursor
movement caused part of the document to be altered. (I have used a text editor
which did exactly this!) Again the limitation that the cursor movement does
not alter the document is sufficient (with others in this case) to make the
non-determinism acceptable.
We have just argued, that to a large extent controlled non-determinism can
be acceptable non-determinism. Every user manual uses this fact, as it defines
only the external behaviour of the system. So, for instance, different versions
of a word processor could use different algorithms, be written in different
programming languages and even run on different hardware (in the same box!)
Similarly, formal specifications define only the interface behaviour leaving
the internals undetermined. Thus all specification is a use of non-determinism.
It is usually assumed that the systems described by formal specifications will
be deterministic. It is just which particular consistent system chosen that
is non deterministic. One could certainly have non deterministic systems which
satisfy a given loose specification, but this is not usually done. There is
a paradox here, in order to make accurate statements about a system (and hence
reduce non determinism regarding its behaviour) specifications are used which
are non determinstic.
Extra material not in the printed chapter
Stretching our imagination a little further, we could say that when we
see a statement " The situation gets even more interesting if the procedure were something like
There is also a strange the duality of non-determinism within the interface.
The computer system must, if it is to be useful, be non deterministic. A completely
deterministic system would never tell the user anything that the user didn't
know already. Not very useful! On the other hand, from the computer's point
of view, the user is non deterministic, but if the user were not so, the system
would always produce the same result. There is conflict between the two partners'
search for determinism, and the programmer usually has the upper hand: forcing
the user to answer in specified ways and in specified orders. From the programmer's
point of view this could be thought of as producing a more deterministic response
from the user. From the user's point of view this is at best restrictive, and
possibly may seem non-deterministic because the programmer's arbitrary decisions
may have little relevance at the interface. Thimbleby calls this excessive control
by the programmer over-determination, [Thimbleby
1980] and elewhere I have proposed a technique for returning control
of the dialogue sequence back to the user. Not surprisingly this technique involves
programs with non-deterministic semantics and which regard the user as a non-deterministic
entity.
We could distinguish two aspects of interface non-determinism based on the
previous discussion. First are those that are part of the application, necessary
to make the application useful. Second are those in the interface, resulting
from arbitrary decisions and complexity, which are not wanted. On the other
hand, we could use this to make the distinction between application and interface,
discussed by Cockton [Chapter 8 of this book]
by saying that the application is what we want to be non-deterministic and
the interface is what we want to be deterministic.
We have seen how the user helped by the designer can avoid, resolve and
control the non-determinism of interactive systems. We have also seen that
non-determinism can be used in formal specification. Earlier we asked whether
non-determinism existed at the user interface or whether it was just a formal
trick, and decided that yes, it is a real, meaningful phenomenon. We could
parallel that now and ask: is the use of non-determinism just a formal trick
for interface specification or can it really be used to improve user interfaces?
The next section will seek to answer that question.
So far we have dealt with cases where non-determinism has unintentionally
arisen in the interface, and we have been mainly interested in removing it
and its problems. In the last section, we saw that when developing systems,
non-determinism can actually be used to good effect. In this section, we will
consider a display update strategy that is deliberately non-deterministic.
We will call this strategy non-deterministic intermittent update It
has considerable advantages over deterministic strategies from the point of
view of efficiency, however can such a deliberate policy of non-determinism
ever be acceptable?
In the first subsection we will consider a basic semi-formal framework in
which we can consider update strategies. In the following sub-section, we will
consider the expression in this framework of total and intermittent update strategies
(see Chapter 4 of [Dix 1987b]). Then, in section 4.7.2 we extrapolate these strategies
and define non-deterministic intermittent update. Finally we consider whether
or not it is an acceptable strategy from the user's point of view, and conclude
that by deliberately adding non-determinism to the interface we may actually
reduce the perceived non-determinism.
Many interactive systems can be considered in the following manner: there
is an object, ( The earlier discussion on specification would lead us to question; what
are the requirements for this update sequence. Typically they fall
into two categories:-
The designer will (more or less) have an idea of which static and dynamic
requirements are important for the particular system, however these will rarely
specify the map completely and thus additional ad hoc requirements will be
added to define it uniquely. (This is idealised, as often in practice these
fundamental design decisions are made as the system is coded, with little
reference to global impact). The additional requirements may themselves be
either static or dynamic.
Bernard Sufrin's specification of a display editor [Sufrin
1982] deliberately leaves the specific update strategy only partially
defined, instead he supplies a static consistency requirement and a dynamic
"inertia" requirement that if the new cursor fits on the old display frame
then the frame doesn't change. Many editors follow this rule of thumb and
add additional rules to fully specify the case when the cursor does not fit
on the old screen, such as "scroll just enough to fit in the cursor", "scroll
a third of a screen in the relevant direction" or "centre the cursor in the
new display". All these rules have additional special cases at the top or
bottom of the text, and in the case of the first two, when the movement of
the cursor is gross.
As already noted in section 4.5.1 the time taken to compute the new map
and update the display may lead to apparent non-determinism for the user,
such as cursor-tracking. Clearly we want to avoid this non-determinism.
If, after all other optimisations have been tried, the response is still
unacceptable, a possible course is to use intermittent update as described
in the last chapter. This corresponds to surpressing some of the displays
in the sequence:
This is mildly non-deterministic in that the sequence if displays is different
depending on exactly how fast the user types. So we already we have a (common)
example of deliberate use of non-determinism.
However, although this reduces traffic to and from the display device (critical
on older low bandwidth channels), it still leaves the considerable expense
of updating the map component. Is there any way we can reduce this overhead?
When specifying the editor component of a simple hypertext system [Dix,
Harrison and Miranda 1986] a slightly different approach to the standard
display inertia was taken. As usual only basic static requirements were specified,
and then to try a few additional requirements that could loosely be described
as "cursor inertia". The first of these was strict cursor inertia, where the
cursor position on the screen moved as little as possible, this is a dynamic
requirement. This had some very strange consequences, in particular, as the
cursor began at the top of the document and hence at the top of the screen,
it always tried to stay at the top of the screen! A second variation
on this was to always position the cursor as near the middle of the screen
as possible. In terms of its observed behaviour this requirement has its own
advantages and disadvantages, however the important thing about it is that
it is a purely static requirement. This means that the display map can always
be calculated from the current text alone, it is a purely declarative interface
In principle one would expect a declarative interface to be very predictable.
However, few interfaces adopt this style. Harold Thimbleby's novel calculator
[Thimbleby 1986] does so, but users are
often surprised at its features, perhaps because they are unused to the declarative
style. The big advantage in performance terms of a declarative interface is
that when one only updates the display intermittently, one need only update
the map intermittently also.
Can we do the same for a non-declarative interface?
It is usually the case, (and is so in the text editor example), that static
consistency is most semantically important. Therefore we could imagine bunching
a series of commands, updating the object and then re-establishing the display
map based on static consistency, and modifying the dynamic requirements to
apply to these consistent epochs.
Previously we would have demanded for each command,
What sort of effect would this have in practise? Imagine the text editor
with display inertia. The cursor is on the second to last line of the screen,
and we slowly enter "down, down, up", at the second "down" the screen would
scroll to accommodate the new cursor position, then on the "up" it would stay
(by display inertia) in this new position. If however we entered the commands
quickly and they were bunched for processing, then after the three commands
when the static and dynamic invariants are enforced, the new cursor position
is within the original display frame and this is retained ... the result is
non-deterministic!! Comparing this to intermittent update, we see that in
that case only the intermediate states of the screen differed, in this case
the final state differs depending on the exact timing of input.
I would argue that the non-determinism introduced is acceptable for two
reasons. Firstly because it is only non-deterministic within the bounds of
the static consistency. Secondly, the exact operation of the dynamic requirements
are usually unpredictable anyway, and thus the apparent non-determinism will
be no worse, and we may actually reduce it. This is especially true of the
principle of display inertia. The reason why it is introduced is to ensure
that the location of useful information changes as little as possible in order
to aid visual navigation. If intermediate displays are not produced then the
deterministic strategy leads to a changing display, whereas the non-deterministic
strategy leads to a fixed one; clearly the latter application of the principle
is more in line with its intention, and for the user is probably more predictable
than its application to imaginary intermediate displays.
We have seen how formal non-deterministic models are useful in describing
interactive systems behaviour. We asked ourselves whether this had any real
meaning. In section 4.4.3 we saw that the appropriate user centred definition
of non-determinism was a behavioural one, and under this definition interfaces
did display non-deterministic properties. Further we have seen many examples
of how non-determinism arises in practice. In section 4.6 we found that users
have many ways of dealing with non-determinism, and that the designer can
design systems to aid them in this. Finally we have seen that it can in fact
be beneficial to deliberately introduce non-determinism into the user interface,
both to achieve other goals (in the example efficiency) but also to potentially
reduce the non-determinism of the interface.
What have we gained by this analysis?
Firstly, by using the strong word non-determinism rather than weaker ones
like unpredictable, we see rather more the urgency of the problems considered.
Secondly, we have found that many different well recognised problems can
be considered as manifestations of non-determinism, this allows the possibility
of cross-fertilisation between the domains.
Thirdly, by considering problems in this light, it enables us to see more
clearly ways of expressing them. For instance, regarding problems of sharing
as specifying acceptable levels of non-determinism. Thus we might describe
a mail system, not in terms of multiple users and messages, but as a single
user with a system displaying limited non-determinism.
Finally, it has given us a more pragmatic view of non-determinism and hence
the ability to consider the idea of deliberately non-deterministic interfaces.
Moving up to the meta-level, it is precisely the way in which the formal
recognition of non-determinism lead us to recognise it as a common problem
that enabled us to approach it in this pragmatic manner. It is also the formal
parallels between the different phenomena that higlighted the parallels at
the informal levels. That is we see formal methods not as a brute force technique
for the aesthetically inarticulate, but as a source of imagery for a thinking
mind.
Thus the input sequence "abc" with different timings may give rise to different
effects
4.2.3 Problem for windowed systems
![]() R
R![]() Λ
Λ ![]() D
D![]() C
C ![]() Λ
Λ ![]() S
S![]() Λ
Λ
Where ![]() Iλ
Iλ
4.3 Non deterministic PIEs
![]()
![]() E
E![]() E
E
![]() p
p ![]() P IND ( p ) = { 0, 1 }
P IND ( p ) = { 0, 1 }
![]() E*
E*
where "::" is sequence concatenation.
![]()
![]() E*
E*
From the multiple independent choice system:
![]() p
p ![]() P IND* ( p ) = { zeroes , ones }
P IND* ( p ) = { zeroes , ones }
where
and
![]() p
p ![]() P IND* ( p ) = { 0, 1 }n+1
P IND* ( p ) = { 0, 1 }n+1
where
Effect history is right length for number of inputs
![]() e*
e* ![]() IND* ( p ): length( e* ) = length( p ) + 1
IND* ( p ): length( e* ) = length( p ) + 1
History cannot change
The first condition says that the effect trace must contain one member for
each input command plus an initial effect, the second that if some sequence
of effects has been the result of a sequence of commands then its first m+1
entries must be a possible result of the initial m commands.
![]() q
q ![]() p
p ![]() P, ep*
P, ep*
![]() IND*
( p )
IND*
( p )![]() eq*
eq* ![]() IND* (q): eq*
IND* (q): eq* ![]() ep*
ep*
where
![]()
![]() p
p ![]()
![]() r
r ![]() P: p=qr
P: p=qr
If any of the ![]() p
p ![]() P || IND*(p) ||
P || IND*(p) || ![]() 1
1
If we had typed "ab" and got the series of responses "111", then there is no
valid response if we typed a further "c".
That is the ND-PIE displays an non-deterministic input language.
The proper additional rule to prevent this is to ensure that for any input
In fact each of the ND-PIEs we derive will satisfy this property.
![]() p
p ![]() q
q ![]() P , ep
P , ep ![]() IND* ( p )
IND* ( p ) ![]() eq
eq ![]() IND* ( q ) st ep
IND* ( q ) st ep ![]() eq
eq
where ![]()
4.3.1 Use for temporal systems
Where
![]() τ
τ
4.3.2 Use for windowed systems
Here ![]() q
q
![]() P { [ doit*
(e, q, λ' ) ] }
P { [ doit*
(e, q, λ' ) ] }
![]() e*
e*
![]() IND*
(p), q
IND*
(p), q ![]() P { e*
:: [ doit* (doit(e* ,c, λ ), q, λ' ) ] }
P { e*
:: [ doit* (doit(e* ,c, λ ), q, λ' ) ] }
![]() IND*
IND*4.3.3 Non-deterministic properties of PIEs
We examined this in the context of the "gone away for a cup of tea" problem,
where one has forgotten exactly what command sequence has been entered before
the cup of tea.
This suggests non-determinism about the value of ![]() p,q,r
p,q,r ![]() P I( p ) = I( q )
P I( p ) = I( q ) ![]() I( pr ) = I( qr )
I( pr ) = I( qr )
If this ND-PIE is deterministic then the PIE is rather uninteresting as its
functionality is independent of the commands entered.
It is a deaf system!
The predictability condition can be stated using this ND-PIE as:
![]() { I* ( p s ) } p
{ I* ( p s ) } p ![]() P
P
This is a measure we could apply to any ND-PIE whether or not it
is derived in this way. It is quite a strong requirement saying that although
the system is non-deterministic, one glance at the first effect resolves all future
doubt. We could of course go on and give non-deterministic equivalents to the
more refined concepts of predictability.
![]() s
s ![]() P , e1* , e2*
P , e1* , e2* ![]() IND* ( s )
IND* ( s )
![]() e1* = e2*
e1* = e2*
If this ND-PIE is deterministic, then ![]() { I ( p ), I' ( p ) }
{ I ( p ), I' ( p ) }
![]() R
R
![]() r
r ![]() R: result ( Ir ( ε ) ) = r
R: result ( Ir ( ε ) ) = r
![]() r, r'
r, r' ![]() R:
R: ![]() prr'
prr'
![]() P:
P: ![]() p
p ![]() P: Ir' ( p
) = Ir ( prr' p )
P: Ir' ( p
) = Ir ( prr' p )
represents non determinism about the starting value of the system. Again we will
later see how this arises informally.
![]() { Ir* ( s ) }r
{ Ir* ( s ) }r ![]() R
R
4.3.4 Summary - formal models and non-determinacy
4.4 Can computer systems be non-deterministic?
4.4.1 The tension for the user
4.4.2 Levels of non-determinism
4.4.3 Behavioural non-determinism
4.5 Sources of non-determinism
4.5.1 Non-determinism due to timing
4.5.2 Non-determinism due to sharing
4.5.3 Data uncertainty
4.5.4 Procedural uncertainty
4.5.5 Memory limitations
4.5.6 Conceptual capture
4.5.7 Discussion
4.6 Dealing with non-determinism
4.6.1 Avoid it
4.6.2 Resolve it
4.6.3 Control it
4.6.4 Use it
y := x * x" in a program the value assigned
to "y" is non-deterministic because, regarding that statement
in isolation, the exact value of "x" is unknown and only
the relationship between "x" and "y" is known.
This is particularly relevant when "x" is a global variable
and hence may have been changed non-locally and hence its exact value
may be difficult to determine. Similarly in the function:
We could say that it uses limited non-determinism to specify the function. The
value of the parameter is unknown and only the relationship between parameter
and result is determined. Comparing the two examples, we could say that the
move from imperative to pure functional programming languages is a trade between
non-determinism induced by sharing and parameter value non-determinism!
real square( x )
real x;
{
return x*x ;
}
is_prime?, taking a number and telling whether or not it is prime.
In this case, the parameter value would be non-deterministic from the point
of view of the procedure and the result from the point of view of the caller.
Both sorts of non-determinism are necessary for the system to be useful. This
parallels within the computer, the duality of non-determinism at the interface.
4.6.5 Summary - informal analysis
4.7 Deliberate non-determinism
4.7.1 Static and dynamic consistency
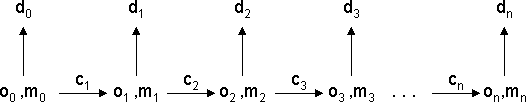
4.7.2 Intermittent update
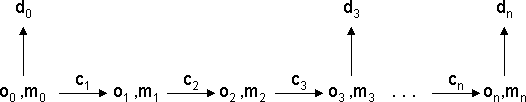
4.7.3 Non-deterministic intermittent update
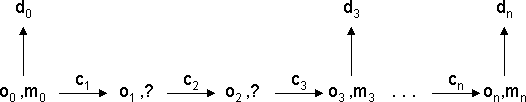
4.7.4 Is it a good idea?
4.8 Discussion
References
full paper
(html)
full paper (html)
D.Phil. Thesis, YCST 88/08, Department of Computer Science, University of
York.
(see also my book Formal
Methods for Interactive Systems)
http://www.hcibook.com/alan/papers/nond90/